What is KPI?
KPI stands for Key Performance Indicator, which is a type of performance measurement commonly used by an organization to evaluate its success of a particular function or activity. It is common for a company to have several performance measurements or KPIs. It is important that a company balance KPIs across several processes rather than have one overriding goal. For example, if KPIs are centered only on production goals then several other worthwhile goals, such as quality, will likely be sacrificed resulting in unbalanced performance measures and hence unbalanced company performance.
Introduction
Stonemont software is widely used across the construction material industry to manage quality information. Hence, it made sense to develop a Quality KPI that could be used effectively by aggregate, asphalt, and concrete producers. The Stonemont Quality KPI is intended to provide an indication of quality; a single value that can be used to quickly assess or compare quality from the parameter level to the company level. Our primary goal with the Stonemont Quality KPI is to provide an indication of future risk regarding conformance to specifications. For this purpose we roll-up four (4) statistical measures. Certain measures have a greater impact on the KPI than others. In fact, one could question why we use these four measures when clearly some are more important than others. In some cases, producers would rather rely entirely on conformance to specifications (CTS). In other cases, producers would rather rely entirely on percent within specifications (PWS). However, we decided to utilize these four statistical measures because we feel they provide more insight into quality when viewed together as a group than when viewed by themselves. For those users that wish to only use PWS we provide a capability report that is similar to the KPI report.
Each of the performance measures are easily computed and most utilize the mean and standard deviation of a given dataset. The arithmetic mean (average) is the expected value or central tendency of a random variable, which in this case is our dataset of a quality parameter. The standard deviation (SD) is a measure of variation or deviation around the mean (Figure 1). A low standard deviation generally indicates less variation and hence more product consistency. A higher standard deviation indicates more variation and hence less product consistency. Although standard deviation can provide some insight into product consistency, it should be viewed relative to the specifications and the ability of the process to produce material in specification. For example, consider the same aggregate product that is produced at a traditional plant versus a fractionated plant. In general, material at the fractionated plant may show a lower standard deviation and hence more product consistency. However, if the material at the traditional plant is produced near the center of the specification while the material at the fractionated plant is produced near a specification boundary it may in fact be that the material at the traditional plant results in less risk of producing material out of specification.
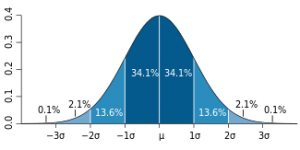 |
| Figure 1. Standard Deviation. |
Each of these statistical measures (except CTS) comes with the standard statistical assumptions regarding normality, sample size, in control processes, etc. The assumptions may not be valid in all cases and for all parameters. However, in many cases they will provide assistance in indicating the risk of future non-conformance to specifications. One of our reasons for using these performance measures for the Quality KPI is that the mean and standard deviation of datasets can be quickly and easily computed using standard database functions. This is important when you consider large companies with hundreds of plants and thousands of products. Although the Stonemont KPI is a quick tool that can be used by management as a relative measure of quality between products or plants, for example, it is no substitute for the routine use of run charts or statistical process control charts to properly assess the performance of each product/process.
The Stonemont KPI can be applied across the aggregate, asphalt, and concrete businesses and therefore includes the flexibility to assign different parameters to comprise the KPI for any given product. For example, an aggregate producer may specify certain gradation sieves and possibly FM to be included in the KPI for a concrete stone. An asphalt producer may consider gradation sieves and asphalt and voids content as KPI parameters for an asphalt mix. A concrete producer would consider values such as compressive strength and possibly other field measured values like unit weight and slump as KPI parameters on a concrete mix. KPIs are most useful when thought is put in regarding what parameters best represent the quality of a product.
Performance Measures
PWS – PWS is equivalent to the Transportation Research Board (TRB) definition of PWL which is as follows: Percent within limits (PWL). The percentage of the lot falling above the LSL, beneath the USL, or between the LSL and the USL. [PWL may refer to either the population value or the sample estimate of the population value. PWL = 100 – PD]. PD stands for percent defects and is commonly 5 or 10 resulting in an acceptable PWL of 90 or 95 and greater. The reason we refer to PWS rather than PWL is because we can compute this statistical measure against specifications (PWS), targets (PWT), and limits (PWL).
PWS is considered a “measure of choice” statistic by the FHWA, meaning that it is the recommended statistic to be used by agencies to measure the quality of pavement material and hence then acceptance of pavement material. PWS is the most important measure in the KPI and can in fact be used by itself as a KPI. We chose to include other statistics in the KPI because they lend insight into why a PWS may be low. PWS is a type of variable acceptance procedure that is based on computed statistical parameters (mean and standard deviation). PWS uses the sample mean and the sample standard deviation to estimate the percentage of the population that is within the specification limits. It is similar to determining the area under the normal distribution curve (Figure 1). A sample is a subset of the data taken from a larger population or process. In other words, typically you can’t effectively measure the entire population so you measure a subset of the population and you use statistics to predict the quality of the entire process. PWS is an estimate of the probability of conformance to the specification…or the capability of the process to produce material in specification. As such, PWS can be used to estimate the future conformance to specifications as long as the process has not changed.
CTS – CTS stands for conformance to specifications and is a measure of the percentage of sample conformance to specification relative to all samples in the data set. This is a type of pass/fail attribute acceptance procedure that is based on measures that are counted rather than computed. CTS is simple to compute and simple to understand and is not subject to the same assumptions regarding normality as PWS. However, attribute acceptance requires a larger dataset to achieve a similar efficiency regarding the estimate of conformance. Another disadvantage of CTS is that it can easily be manipulated and therefore is not considered a strong predictor of future conformance. So why did we include CTS in the Stonemont KPI? The answer is that we have found that CTS is commonly used and understood in the industry and when used in conjunction with PWS can provide useful information. In general, one would not expect CTS and PWS to significantly differ from one another if the dataset is large enough. However, we have observed cases where PWS is 85% and CTS is 100% indicating that CTS may not be representative of the true estimate of the population conformance to specifications. This can happen for reasons including the dataset being too small or failing samples being removed from the dataset. Regardless of the reason, we consider large discrepancies an indicator of a potential problem that may warrant an investigation to better understand the cause of the discrepancy. We consider a 10% difference between measured (CTS) and predicted (PWS) conformance to indicate a large discrepancy. The KPI is weighted in favor of PWS rather than CTS as the difference between the two numbers increases, unless CTS is lower than PWS. This ensures that a high CTS doesn’t bias the KPI.
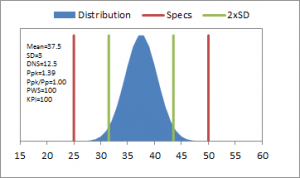
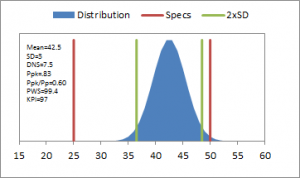
Ppk – Ppk is a process capability ratio that will give an indication of where the process mean is located relative to the specifications. Ppk is another type of variable acceptance procedure that is based on computed statistical parameters mean and standard deviation. Ppk = 1: the mean is 3xSD away from the closest specification; Ppk = 0.67: the mean is 2xSD away from the closest specification; Ppk = 0.33: the mean is 1xSD away from the closest specification; Ppk = 0: the mean is on a specification; Ppk < 0: the mean is outside of specifications. We include Ppk in the Stonemont KPI because where the mean is located relative to the specifications is the primary reason for a low PWS and because it is easy to understand.
The KPI uses a Ppk value of 0.67, which corresponds to the process mean being two (2) standard deviations away from the closest specification boundary. Statistically this is nearly equivalent to 95% compliance. Ppk values greater than or equal to 0.67 contribute 100% to the KPI. Ppk values less than 0.67 contribute less than 100 % to the KPI. Remembering these key Ppk values can provide important information regarding how your process is performing relative to specifications. Values less than 0.67 indicate your closest specification is less than 2xSD away from the mean, which indicates that your risk of producing nonconforming material or defects is greater than 5% and therefore your KPI is lower.
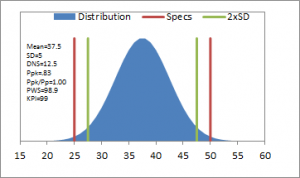
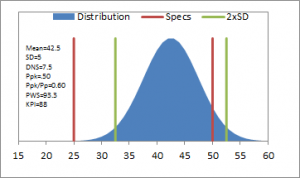
Ppk/Pp – Pp is a measure of the spread of the specifications relative to the spread of the process. Used by itself it doesn’t indicate where the process mean is located relative to specifications. As a result, Ppk/Pp is used to give an indication of how off-center the process mean is located relative to the specifications. In general, the more off-center the process mean, the higher the risk of non-conformance. Ppk/Pp = 1: The mean is centered within the specifications; Ppk/Pp = .5: The mean is half way between the center of the specification and the closest specification; Ppk/Pp = .25: The mean is a quarter way from the closest specification relative to the center of the specification. Values of Ppk/Pp greater than 1 are possible and indicate the process is off-center but isn’t a concern when the boundary specification on percent values is 0 or 100. The KPI uses a Ppk/Pp value of 0.5. Ppk/Pp >= .5 contribute 100% to the KPI. Values of Ppk/Pp < .5 start to lower the KPI. Ppk/Pp is not a critical measure of quality on its own. It was included only because it provides a measure that indicated where the mean is relative to the specification. Ppk/Pp is different than just Ppk because although Ppk may indicate that you are less than two standard deviations away from the closest specification, it doesn’t indicate whether you are near the center of the specification (indicating that your process isn’t capable of producing material at 95% conformance due to a large standard deviation or overly tight specifications); or if the mean is too far off-center to produce conforming material.
Summary
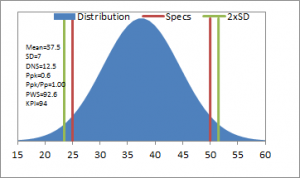
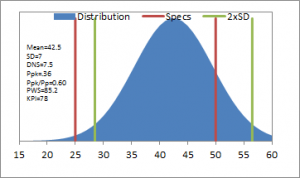
Stonemont Software is widely used to manage aggregate, asphalt, and concrete quality control information and as a result we developed a Quality KPI that can be used across these industries. Many companies use KPI measures to evaluate performance for different sectors of their business. These different KPI values can be combined into a single KPI value but more importantly they can be viewed individually to identify underperforming sectors of the business. The approach we took with the Stonemont Quality KPI had a similar goal in mind in that it can be viewed as a single KPI value but that the components that go into the KPI provide additional information and insight into underperforming KPI values. By presenting all of this information together, the KPI value is better understood. Figures 2-7 show simulated dataset distributions with specification boundaries and 2xSD limit boundaries. Figures 2-4 demonstrate how the KPI changes when a mean is centered relative to the specifications but standard deviation increases. Figures 5-7 show how the KPI changes when a mean is off-center relative to the specifications for different standard deviations. These charts show that as the standard deviation increases the risk of producing non-conforming material can increase but that this risk is much greater when the distribution mean is sufficiently off-center relative to the specifications. Our primary goal with the Stonemont Quality KPI is to provide an indication of future risk regarding conformance to specifications. Note that the Stonemont KPI is useless on small datasets and should not be used for daily or even weekly process control, which is the intended function of run charts and control charts. However, the Stonemont KPI is a measure that producers can use to improve their processes by helping to identify material that has an increased risk of non-conformance.
Adrian Field